Reverse Engineering Crypto Functions: RC4 and Salsa20
25 August 2021
By Jacob Pimental
Many malware samples use encryption for Command and Control (C2) communications, encrypting files, string obfuscation, and many other tasks. It can be challenging to know which encryption algorithm you are looking at when analyzing a sample. This post aims to teach newer analysts about common encryption algorithms, how they work, and how you can identify them when reverse engineering.
RC4 Algorithm
How it Works
RC4’s internal state is an array of 256 bytes, denoted as S[], ranging from 0-255. RC4 will use its Key Scheduling Algorithm (KSA) to randomly swap the bytes in S[] using the user inputted key as the seed. S[] is then used to generate a keystream via the Pseudo-Random Generation Algorithm (PRGA). This keystream, denoted as KS[], is the same size as the plaintext input. Finally, RC4 will XOR the keystream by the plaintext to create the encrypted ciphertext.
Key Scheduling Algorithm (KSA)
The Key Scheduling Algorithm for RC4 will take the internal state referenced earlier, denoted as S[], and permutate it based on a key the user inputs. For each index in S[], the algorithm will swap the value with another index of S[] based on the value: (j + S[index] + key[index % keylength]) % 256, where j has a starting value of zero. This can be shown in the following Python code:
def KSA(key):
"""Rearranges the values in an array of 256 bytes based on key.
Params:
key (str): Key used to permutate the bytes
Returns:
list: A permutation of 256 bytes used to generate keystream
"""
S = [i for i in range(256)] # Initialize array of 256 bytes
j = 0
for i in range(256):
k = ord(key[i % len(key)])
j = (j + S[i] + k) % 256 # Calculate index to swap
S[i], S[j] = S[j], S[i] # Swap values in the array based
return S
Pseudo-Random Generation Algorithm (PRGA)
The output from the Key Scheduling Algorithm is used to generate a keystream using RC4’s PRGA. This keystream will be the same size as the plaintext input and is generated by taking the value at S[i + 1], and swapping that with the value of (j + S[i + 1]) % 256. For this example, i is all numbers from zero to the length of the plaintext and j is zero. After this swap, the value S[ (S[i] + S[j]) % 256 ] is appended to the keystream, thus creating a pseudo-random list of bytes. This can be shown in the following Python code:
def PRGA(S, amount):
"""Pseudo-Random algorithm that creates the final keystream used to encrypt.
Params:
S (list): The 256 byte array generated by KSA
amount (int): Length the keystream needs to be (size of plaintext)
Returns:
list: The final keystream used for encryption
"""
j = 0
K = []
for i in range(amount):
i = (i + 1) % 256
j = (j + S[i]) % 256
S[i], S[j] = S[j], S[i]
K.append(S[(S[i] + S[j]) % 256])
return K
Putting it All Together
Once the keystream is generated, the RC4 algorithm will use it to encrypt the plaintext input by XORing the bytes together. Decryption works by deriving the same keystream using the original key and XORing that by the ciphertext. This entire process is shown in the following Python code:
def XOR(pt, k):
"""XORs two arrays together.
Params:
pt (list): The plaintext array
k (list): The key to XOR by
Returns:
list: The ciphertext
"""
ct = []
for i in range(len(pt)):
ct.append(ord(pt[i]) ^ k[i])
return ct
def RC4(plaintext, key):
"""Main RC4 function.
Params:
plaintext (str): The plaintext to encrypt
key (str): The key used for encryption
Returns:
list: List of encrypted bytes
"""
S = KSA(key)
print(S)
K = PRGA(S, len(plaintext))
print(K)
ct = XOR(plaintext, K)
return ct
Identifying RC4 in Assembly
An easy way of identifying that an application is using the RC4 algorithm is by looking for the value 256 when the algorithm is creating the initial state (S[]). This normally occurs in two loops that run 256 times each and will be either creating or modifying an array.
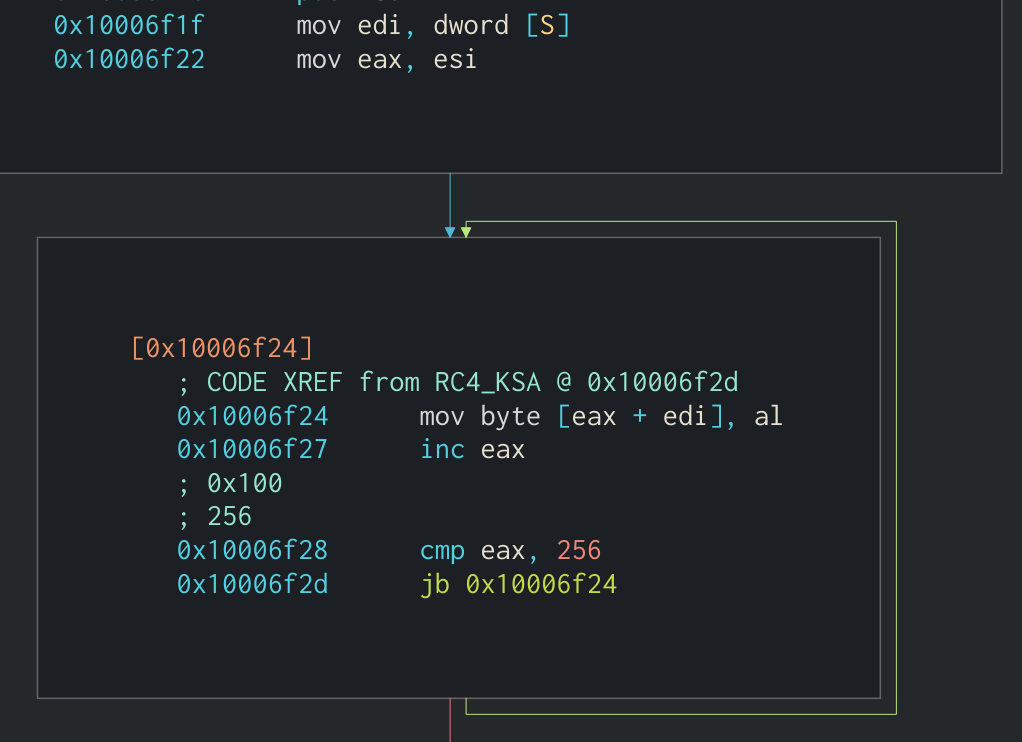Loop that creates initial S array of bytes from 0 to 255
It is important to notice that in the second loop in RC4’s key scheduling algorithm the bytes in S[] will be swapped around. You can see this in the following screenshot:
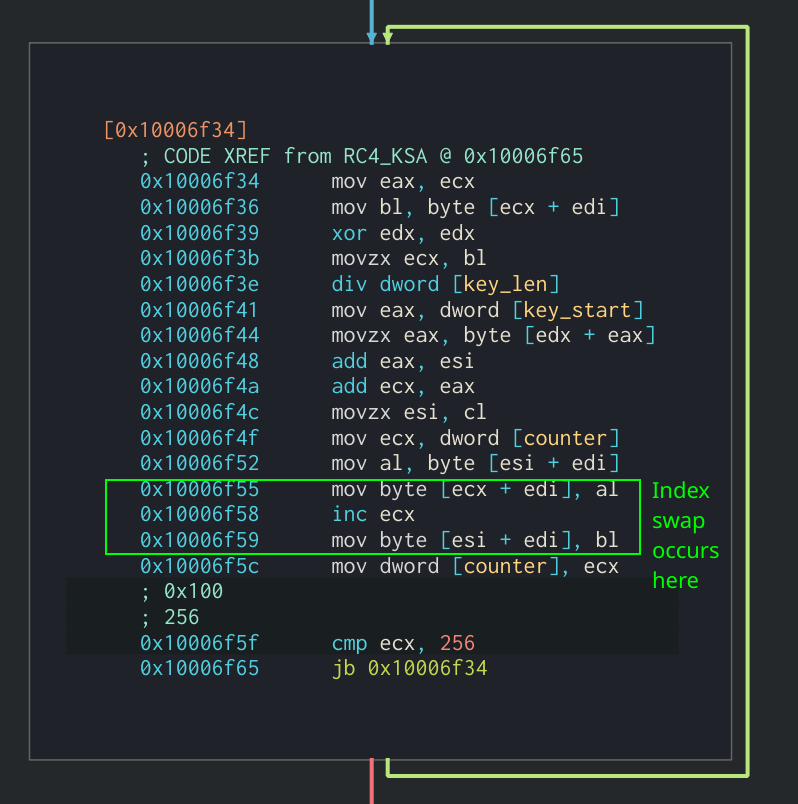Second loop in S array creation that swaps bytes
You can also identify RC4 by its pseudo-random generation algorithm. Two important things to notice here are the use of the previously created S[] variable and the XOR operand being used. Keep in mind that this section will be looped by the length of the plaintext, not 256 times like the KSA.
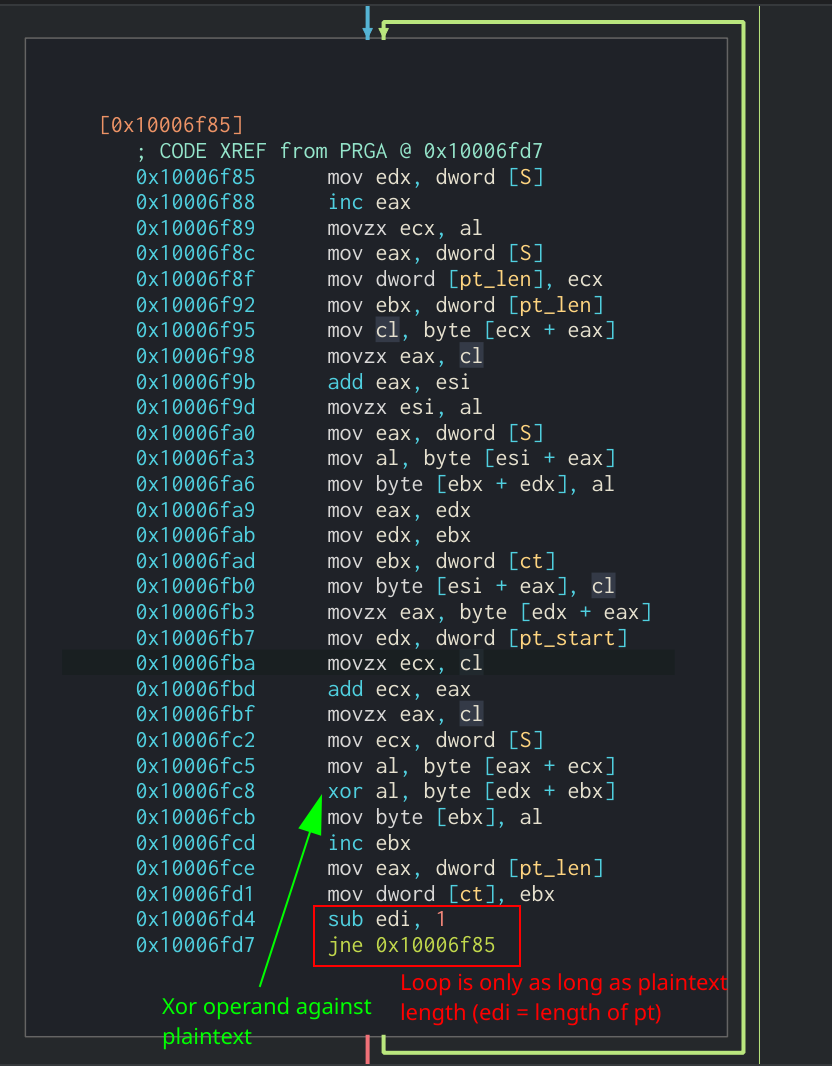Main loop used for RC4 PRGA
By identifying both functionalities in the code, it is safe to say that this is the RC4 algorithm. This particular example was from my analysis of the Sodinokbi Ransomware in a previous post.
Salsa20 Algorithm
How it Works
Salsa20 works by encrypting data in 64 bytes “blocks”. The algorithm is counter-based, meaning that a counter variable is used when generating the key depending on which “block” of data is being encrypted. The internal state of Salsa20 consists of an array of 16 32-bit words that can be shown as a 4x4 matrix:
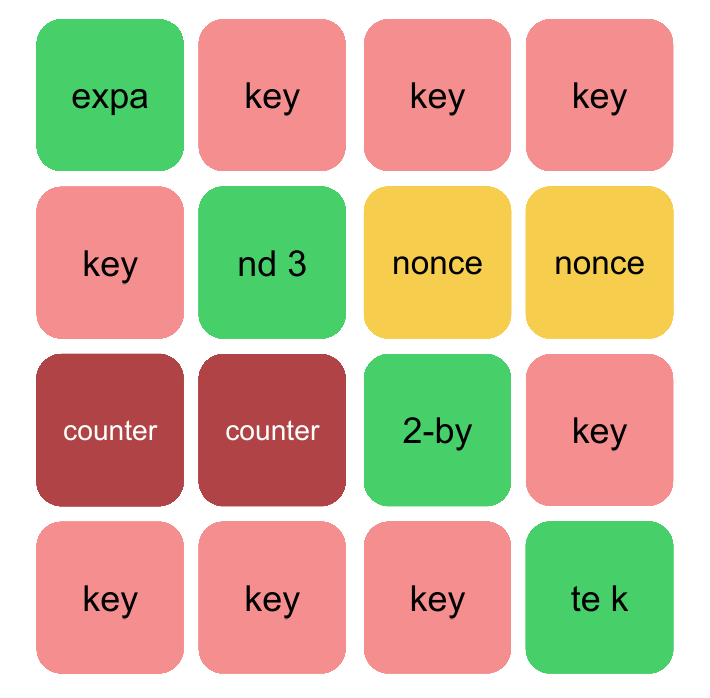Salsa20’s initial state
This state then undergoes a “quarter-round” function which randomizes the values in the matrix. Once the state is run through this function multiple times, normally 20, the final result is then added back to the initial state’s values. This becomes the keystream that will be XOR’d against 64 bytes of the plaintext data. Finally, the counter variable will be incremented and the process starts again with the next 64 bytes.
State Generation
The initial state for Salsa20 consists of 16 32-bit words consisting of the following:
| State variable | Description |
|---|---|
| Key | 16 or 32 byte key defined by the user |
| Nonce | Eight byte nonce value that can be randomly generated or given |
| Counter | The counter variable that denotes which “block” is being encrypted |
| Constant | Constant value of either “expand 32-byte k” or “expand 16-byte k” depending on the length of the key |
If the length of the key is 32 bytes, then it is split between the two sets of four 32-bit words in the state with the first 16 bytes in the first set and the last 16 bytes in the second. Otherwise, if the length of the key is 16 bytes it is repeated between the two sets of four 32-bit words. The state generation can be defined in the following Python code:
def setup_keystate(self, key, nonce, counter=0):
"""Sets up initial keystate for Salsa20.
Params:
key (bytes): Key used to encrypt data (16 or 32 bytes)
nonce (bytes): One-time pad used to generate keystate
counter (int): Determines which blok is being encrypted
"""
nonce = list(struct.unpack('<2I', nonce)) # Splits nonce into 2 words
count = [counter >> 16, counter & 0xffff] # Generates high and low order words for counter
if len(key) == 32:
const = list(struct.unpack('<4I', b'expand 32-byte k')) # Splits const into 4 words
k = list(struct.unpack('<8I', key)) # Splits key into 8 words
self.state = [const[0], k[0], k[1], k[2],
k[3], const[1], nonce[0], nonce[1],
count[1], count[0], const[2], k[4],
k[5], k[6], k[7], const[3]]
elif len(key) == 16:
const = list(struct.unpack('<4I', b'expand 16-byte k'))
k = list(struct.unpack('<4I', key)) # Splits key into 4 words
self.state = [const[0], k[0], k[1], k[2],
k[3], const[1], nonce[0], nonce[1],
count[1], count[0], const[2], k[0],
k[1], k[2], k[3], const[3]]
An example of how the state would look with a 16 byte and 32 byte key can be seen below:
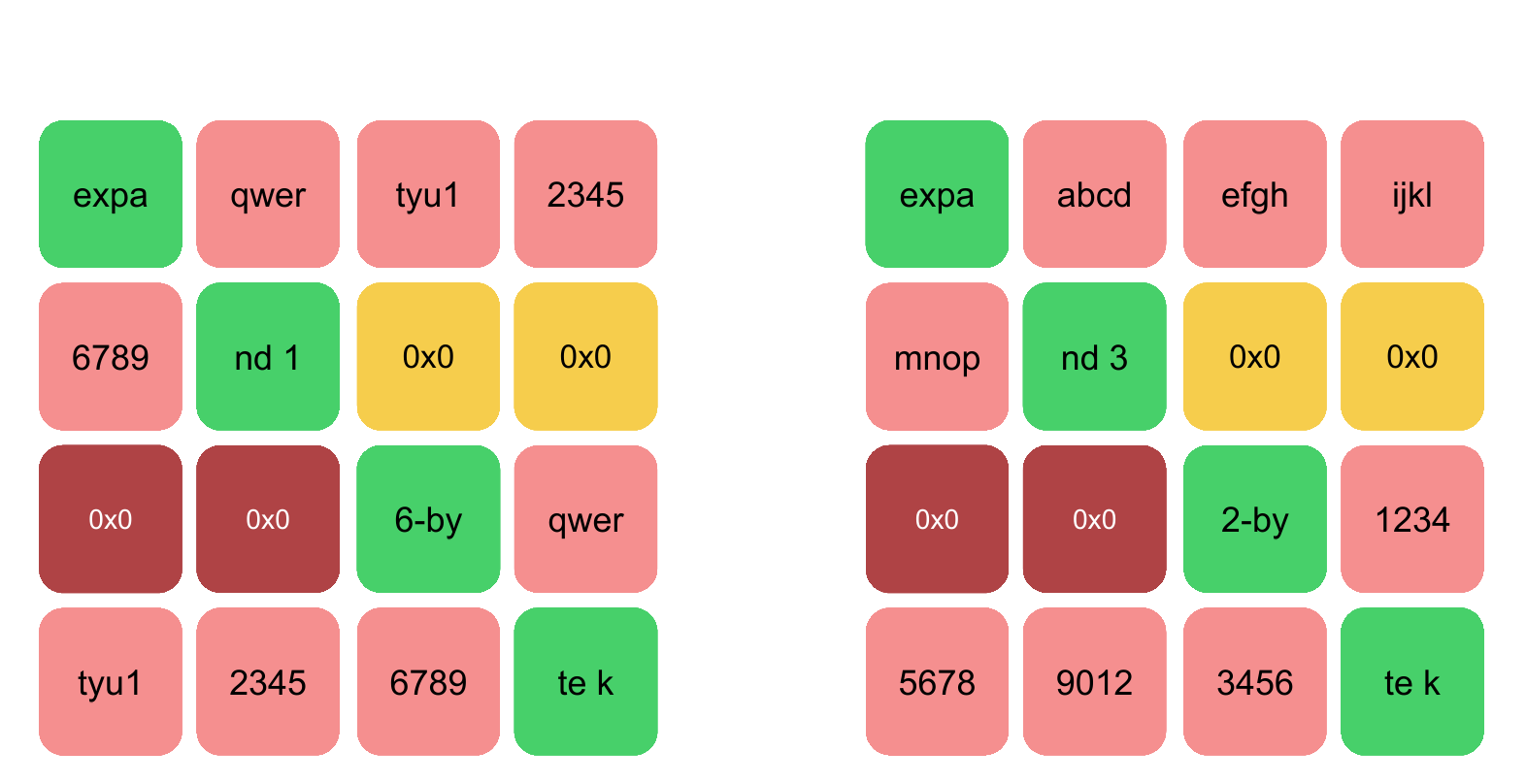Difference between 16 and 32 Byte key in Salsa20
Generating Keystream
To generate the keystream, Salsa20 uses a “quarter-round” function to randomize the data in its initial state. This function is called “quarter-round” as it is working on one column or row at a time out of four, or one “quarter” at a time. The default number of “rounds” is 20, unless otherwise specified. On even rounds, the algorithm will transform its column values using the quarter-round function and on odd rounds it will transform its rows. The quarter-round funtion can be shown in the following Python code:
def QR(self, x, a, b, c, d):
"""quarter-round function used in Salsa20.
Params:
x (array): Starting array to permutate
a (int): index value for array
b (int): index value for array
c (int): index value for array
d (int): index value for array
"""
x[b] ^= rol((x[a] + x[d]) & 0xffffffff, 7)
x[c] ^= rol((x[b] + x[a]) & 0xffffffff, 9)
x[d] ^= rol((x[c] + x[b]) & 0xffffffff, 13)
x[a] ^= rol((x[d] + x[c]) & 0xffffffff, 18)
Once the initial state is run through this permutation function for the number of rounds specified, it will then add the newly randomized state to its original values. This will ensure that the process cannot be reversed and the key cannot be recovered. The entire keystream generation process looks like:
def generate_ks(self):
"""Generates Keystream for Salsa20
Returns:
bytes: 64-byte keystream
"""
x = self.state[:]
for i in range(10):
self.QR(x, 0, 4, 8, 12)
self.QR(x, 5, 9, 13, 1)
self.QR(x, 10, 14, 2, 6)
self.QR(x, 15, 3, 7, 11)
self.QR(x, 0, 1, 2, 3)
self.QR(x, 5, 6, 7, 4)
self.QR(x, 10, 11, 8, 9)
self.QR(x, 15, 12, 13, 14)
out = []
for i in range(len(self.state)):
out.append((self.state[i] + x[i]) & 0xffffffff)
out = struct.pack('<16I',
out[0], out[1], out[2], out[3],
out[4], out[5], out[6], out[7],
out[8], out[9], out[10], out[11],
out[12], out[13], out[14], out[15])
return out
Putting it All Together
After the keystream is generated, the Salsa20 algorithm will XOR it by the first 64 bytes, or less, of the plaintext. If there is more than 64 bytes in the plaintext data, then the counter variable is incremented and a new keystream is generated for the next 64 byte block. This process continues until the entirety of the plaintext is encrypted. The Python code for this would look like the following:
def encrypt(self):
ct = []
print(len(self.data))
for i in range(0, len(self.data), 64):
block = self.data[i:i+64]
self.setup_keystate(self.key, self.nonce, i//64)
ks = self.generate_ks()
for x in range(len(block)):
ct.append(block[x] ^ ks[x])
return ct
Identifying Salsa20 in Assembly
The easiest way to identify Salsa20 when analyzing a binary is to look for the constants expand 32-byte k or expand 16-byte k. These will almost always be present for Salsa20 and are a guaranteed indicator.
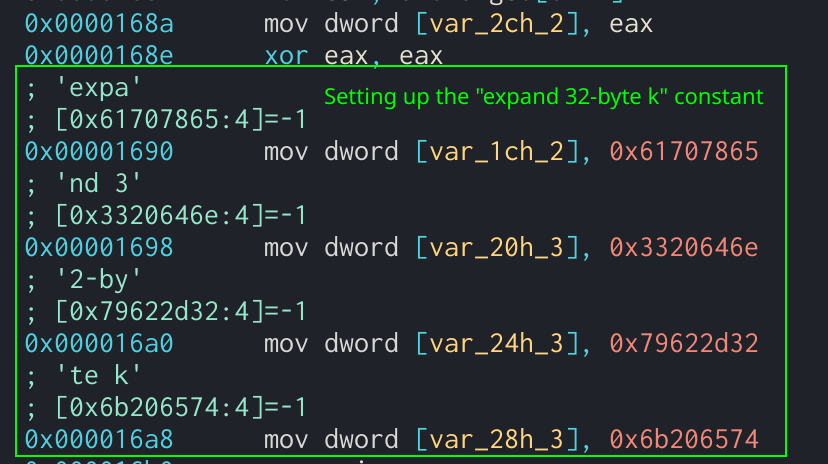Salsa20 constant value being moved into the state
However, in order to evade analysis, the author might change these constant values. If these values are changed, next thing to look for would be the quarter-round function that Salsa20 uses to generate the keystream. To locate this, the analyst should be looking for the rol operands followed by the normal quarter-round values: 7, 9, 13, and 18.
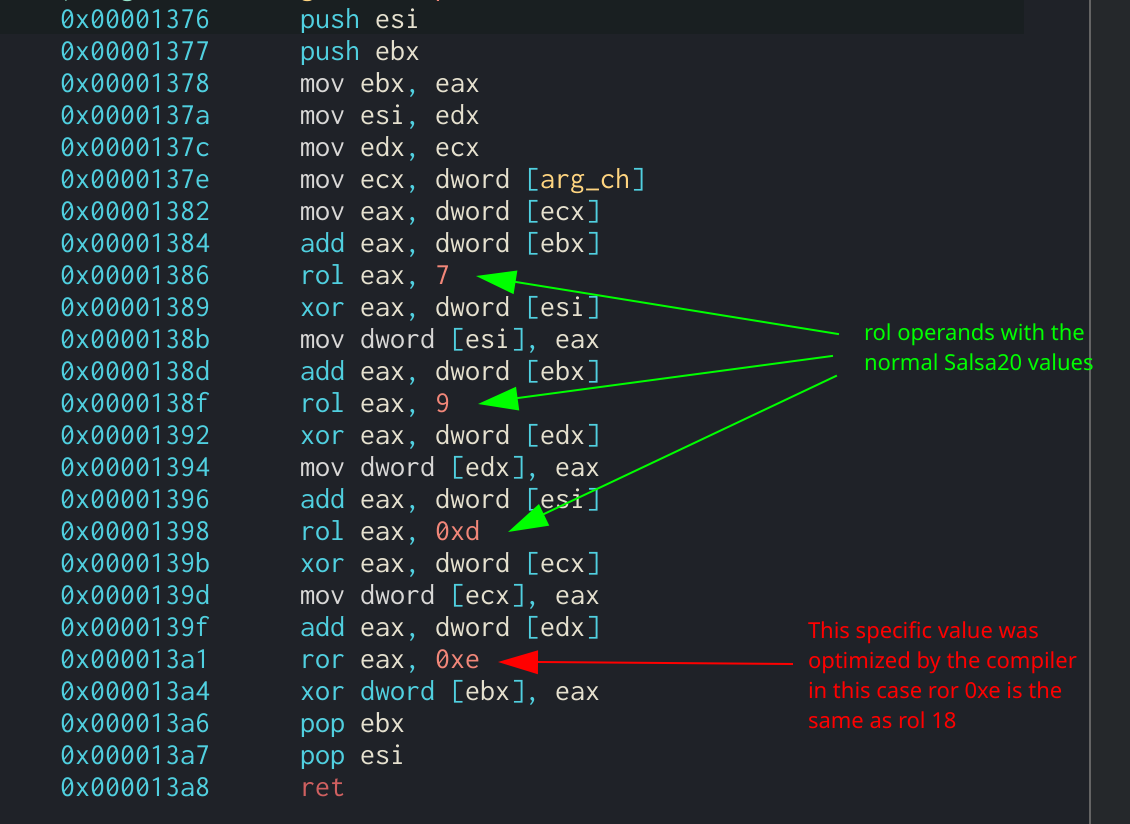Salsa20 quarter-round function showing the rol operands
The examples for this section were from an open source version of the Salsa20 algorithm written in C by alexwebr.
Conclusion
Hopefully this post will help newer analysts in identifying basic crypto functions that can be used by malware. By learning how the algorithms operate at a low level, it will make it easier to spot them in the wild and possibly be able to identify different variations of the same algorithm that an author may use to evade detection. If you have any questions or comments about this post, feel free to message me on my Twitter or LinkedIn.
Thanks for reading and happy reversing!
